Windows CryptoAPI spoofing vulnerability CVE-2020-0601
Windows CryptoAPI spoofing vulnerability CVE-2020-0601
Vulnerability Description
On January 15, Microsoft released a security patch for CVE-2020-0601. This vulnerability was generated by Microsoft when implementing digital certificate verification of elliptic curve encryption algorithm. It can be used to forge signatures or certificates from trusted sources. Its business characteristics will derive a variety of attack vectors, which have extremely high exploitable value and great potential destructive power. Win 10 and Windows Server 2016 & 2019 are also within its scope of impact.
Vulnerability Impact
The Microsoft Windows version of the certificate with the ECC key with the specified parameter, applications that rely on the Windows CryptoAPI
Vulnerability reappears
The root of CVE-2020-0601 is the implementation problem of the elliptic curve encryption algorithm in Microsoft’s encryption library crypt32.dll. First, let’s understand the basic principles of the elliptic encryption algorithm.
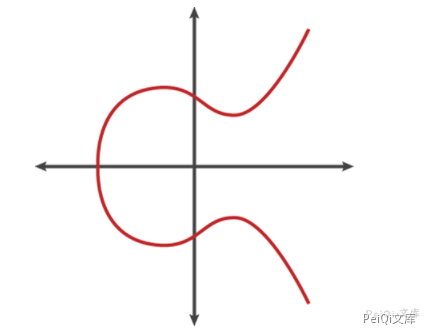
To understand the elliptic curve encryption algorithm vividly, you can look at it in combination with the graph. The following is an equation y2 = x3 + ax + b that conforms to the elliptic curve. The image is as follows:
Some unique properties of elliptic curves make it suitable for encryption algorithms:
- Elliptic curve symmetry about x-axis
Any non-vertical line intersects at most three points with a curve.
- The curve is smooth, that is, there are no two or more different tangents at all points in the curve.
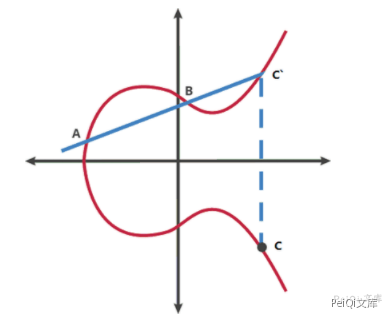
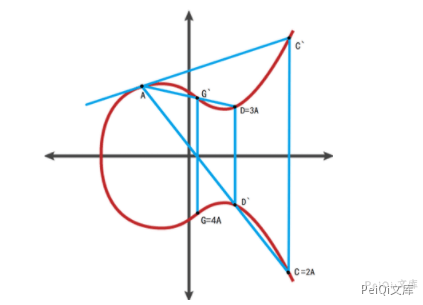
At any two points A and B on the elliptic curve (if A and B overlap, it will be a tangent of A), make a straight line intersect at another point C of the elliptic curve, and make a parallel line of the y-axis through C and intersect the elliptic curve at point C, define A+B=C.
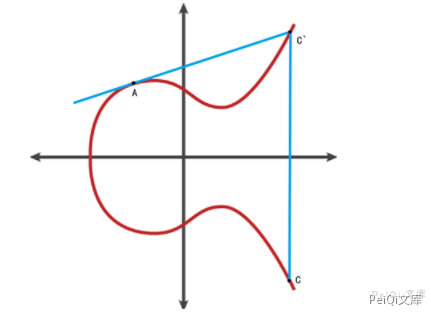
If A and B are the same point, use A to make the tangent of the elliptic curve and obtain the corresponding result C=2A in the same way.
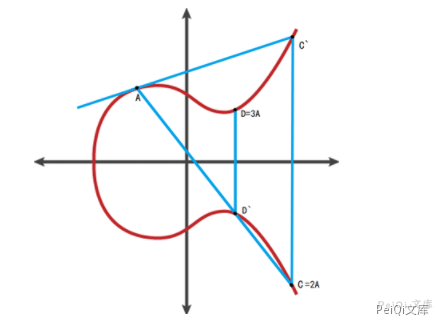
Next is the focus of elliptic curve encryption. If multiple A are accumulated, the connection lines can be accumulated in turn to obtain the value of nA.
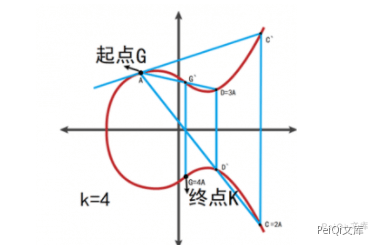
The starting point is A, the end point D=3A, and the order is 3.
The starting point is A, the end point is G=4A, and the order is 4.
Elliptic curve encryption
Consider K=kG, where K and G are points on the elliptic curve Ep(a,b) and n is the order of G.
- Point G is called the base point
k(k<n) is a private key
- K is a public key
Elliptic curve encryption algorithm (ECC) is a public key encryption technology like RSA. It encrypts the original data with a public key and decrypts it with a private key. Even if an attacker obtains the ciphertext and public key, it cannot decrypt (at a reasonable time or cost) to obtain the plaintext.
Similarly, the elliptic curve encryption algorithm (ECC) is also used for digital signatures, generating signatures with private key encryption, decryption of signatures with public keys, and if the original text is the same, the signature verification is successful.
Public key encryption is reliable because they utilize the one-way function principle in the field of public key cryptography. Forward operation is very simple, while reverse operation is very difficult.
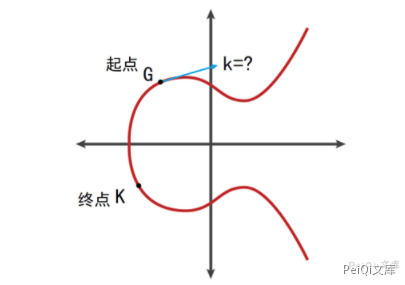
Starting from G (base point), perform k (private key) transformation. As long as you calculate step by step, the value of the end point K (public key) can be easily obtained.
It is known that the starting point G (base point) and end point K (public key), and it is difficult to reversely obtain the number of movements k (private key) (the best algorithm also reaches the full exponential complexity)
Compared with traditional RSA encryption algorithms, elliptical encryption algorithms have inherent advantages, and the reverse process of elliptical encryption algorithms has greater time complexity than RSA.
Shorter keys also mean less storage space, faster encryption and decryption speeds, and less bandwidth consumption. Because of these advantages of the elliptical encryption algorithm, it is used in Windows signature systems, https certificates, Bitcoin systems and China’s second-generation ID systems.
Although the elliptic curve encryption algorithm has many advantages and is extremely difficult to crack purely on algorithm angles, Microsoft’s shortcomings in the implementation of this algorithm provide opportunities for exploitation of vulnerabilities.
In normal standard elliptic curve algorithms, the basis point G is not specified at will, but has a fixed value (the standard function is to specify the selection of parameters such as basis point G). For example, in the secp256r1 version of the elliptic curve algorithm, the basis point G should be a fixed value specified by the standard. If the parameters are not verified, the user can customize the value of the incoming basis point G (as a parameter of the function), the special solution of the above private key k=1 can be established.
This is exactly the case when verifying the function using the ECC algorithm signature part in the vulnerable version of crypt32.dll. The original function was not validated with parameters, and the content of the base point G participating in the calculation was arbitrarily specified by the verified certificate, so that the unauthorized certificate can build a special solution of the private key k=1 to successfully pass the signature verification process of the elliptical encryption algorithm.
Let’s use a POC of CVE-2020-0601 as an example to parse the construction process of false keys:
1
2
3
4
5
6
7
8
9
10
11
12
require 'openssl'
raw = File.read ARGV[0] # 读取使用ECC算法的证书文件
ca = OpenSSL::X509::Certificate.new(raw) # 读取使用ECC算法的证书
ca_key = ca.public_key # 从证书中提取公钥ca_key
ca_key.private_key = 1 # 设置私钥为1,使得公钥K==1*基点G的等式成立
group = ca_key.group
group.set_generator(ca_key.public_key, group.order, group.cofactor)
group.asn1_flag = OpenSSL::PKey::EC::EXPLICIT_CURVE
ca_key.group = group # 利用构建的假基点G和假密钥k设置新group
File.open("spoofed_ca.key", 'w') { |f| f.write ca_key.to_pem } # 将新的group写入文件
The function of the elliptic curve encryption algorithm in the patched Crypt32.dll has been added to the parameter verification part, solving the problem of constructing a second special valid key caused by freely specifying the parameter G.
A mistake in a verification mechanism leads to a chain of trust chains.
The existence of this vulnerability causes the constructed invalid signature to pass the verification mechanism, allowing the supposedly broken trust chain to be exploited, and the guarantee will continue step by step, and ultimately allowing the illegal content to obtain the legal signature identity of the certificate owner.